什么是前缀式，中缀式，后缀式

Posted on Wed, 25 Dec 2024 10:35:10 +0800 by LiangMingJian

概述 #

前后缀式都是使用栈进行储存，遵循后进先出的原则。例如使用栈计算后缀式 xyc + 8 * - 。

1. 栈依序存入 x，y，c
2. 遵循后进先出，取出 c，y，进行加法运算得 y + c，存入栈中，此时栈底为 x，栈顶为 y + c
3. 存入 8
4. 取出 8，y + c，进行乘法运算得 ( y + c ) * 8，入栈
5. 取出 ( y + c ) * 8，x，进行减法运算得 x - ( y + c ) * 8，注意后取出的 x 为被减数

前缀式 #

前缀式又称波兰式，是一种没有括号的算术表达式。其特点是将运算符写在前面，操作数写在后面。例如算式：1 - ( 2 + 3 ) ，等价于 - 1 + 2 3

中缀式 #

中缀式就是平时人们常用的算术表示方法，操作符处于操作数的中间。例如算式：3 + 4

后缀式 #

后缀式又称逆波兰式。与前缀式不同的是，后缀式把运算符写在运算对象的后面。例如算式：a + b，等价于 a b + 。这种写法的优点是，可以根据运算对象和算符的出现次序进行计算，而不需要使用括号，便于机器求值

中缀式转化前、后缀式 #

中缀式可以通过构造二叉树，通过后序遍历二叉树的方法求得后缀式，通过先序遍历二叉树的方法求得前缀式。例如算式： ( 1 + 2 ) * 3 + 2 * 1

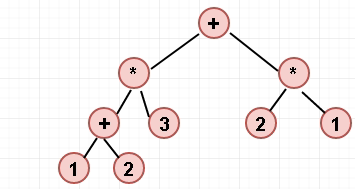
• 后序遍历的实现思想是：从根节点出发，依次遍历各节点的左右子树，直到当前节点左右子树遍历完成后，才访问该节点元素
• 先序遍历的实现思想是：从根节点出发，先访问根节点，再访问当前节点的左子树，若当前节点无左子树，访问当前节点的右子树，直至所有元素被访问
• 中序遍历的实现思想是：从当前节点出发，先当前节点的左子树，再访问根节点最后再访问右子树
• 后序遍历：1 2 + 3 * 2 1 * +
• 先序遍历： + * + 1 2 3 * 2 1
• 中序遍历：( 1 + 2 ) * 3 + 2 * 1