常用的树形结构存储算法
Posted on Wed, 25 Dec 2024 10:13:13 +0800 by LiangMingJian
父子关系算法
父子关系,顾名思义,就是当前节点只关注自己的父节点是谁,并将其保存起来即可,查询我的子节点有那些,只需要全局找到所有父 ID 是和我的 ID 一致的项。
如下图所示:
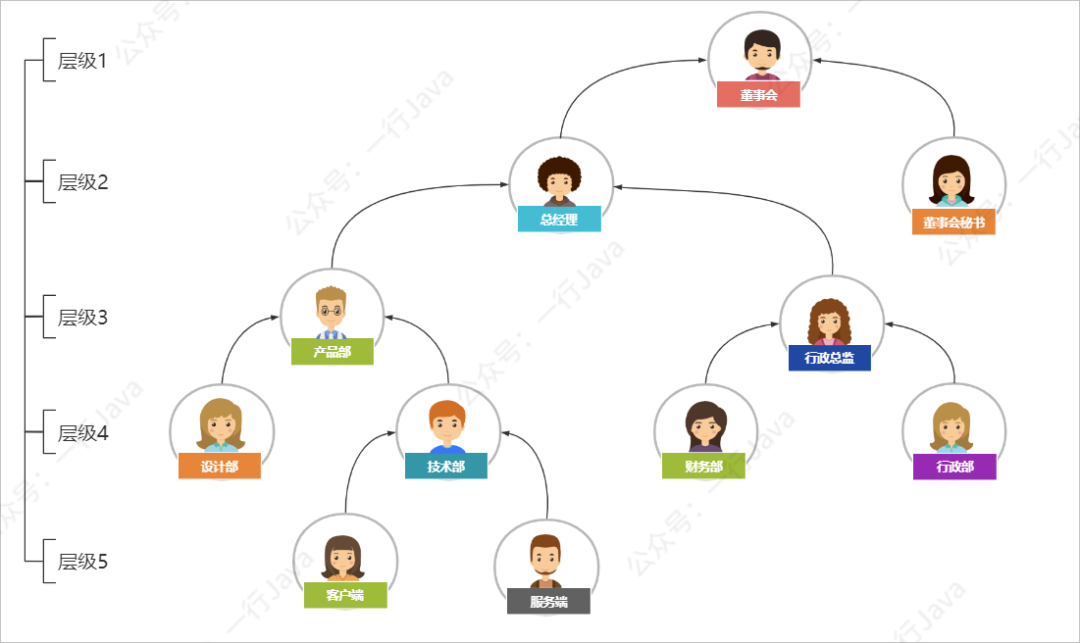
这种算法的优点是:
- 方案简单易懂,数据结构简单清晰。
- 层级直观,鲜明。
- 易维护,层级关系只需要关注自己的父ID,所以在添加、修改的时候,一旦关系发生变化,调整对应的父 ID 即可。
这种算法的缺点是:
- 查找麻烦,统计麻烦,根据当前节点的数据,只能获取到子节点的数据,一旦查询、统计超出父子范围,就只能通过递归逐层查找了。
根据上面的图示示例,与其对应的表结构如下:
| ID | dep_name(部门名称) | level(层级) | parent_id(父ID) |
|---|---|---|---|
| 1 | 董事会 | 1 | 0 |
| 2 | 总经理 | 2 | 1 |
| 3 | 董事会秘书 | 2 | 1 |
| 4 | 产品部 | 3 | 2 |
| 5 | 行政总监 | 3 | 2 |
| 6 | 设计部 | 4 | 4 |
| 7 | 技术部 | 4 | 4 |
| 8 | 财务部 | 4 | 5 |
| 9 | 行政部 | 4 | 5 |
| 10 | 客户端 | 5 | 7 |
| 11 | 服务端 | 5 | 7 |
先序树算法
在先序树算法中,节点不再保存父节点的 ID,而是为每个节点增加左值和右值。
如下图所示:
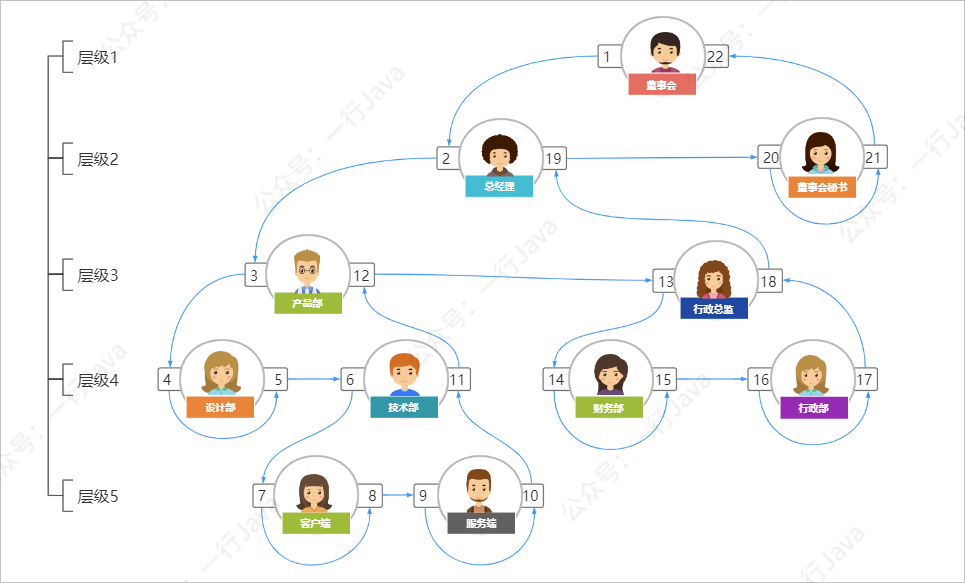
这种算法的优点是:
- 查询汇总简单高效。
- 无需递归查询,性能高。
这种算法的缺点是:
- 结构相对复杂,数据层面理解难度较高。
- 不易维护,因为左右值的存在,会直接影响到后续的节点,因此,当前节点增删改时,都会对后续的节点产生影响。比如在增加节点(A:B)时,需要把所有比 A(新增节点的左数)大的左数全部 +2,所有比 B(新增节点的右数)大的右数全部 +2。
根据上面的图示示例,与其对应的表结构如下:
| id | dep_name(部门名称) | lt(左值) | rt(右值) | lv(层级) |
|---|---|---|---|---|
| 1 | 董事会 | 1 | 22 | 1 |
| 2 | 总经理 | 2 | 19 | 2 |
| 3 | 董事会秘书 | 20 | 21 | 2 |
| 4 | 产品部 | 3 | 12 | 3 |
| 5 | 行政总监 | 13 | 18 | 3 |
| 6 | 设计部 | 4 | 5 | 4 |
| 7 | 技术部 | 6 | 11 | 4 |
| 8 | 财务部 | 14 | 15 | 4 |
| 9 | 行政部 | 16 | 17 | 4 |
| 10 | 客户端 | 7 | 8 | 5 |
| 11 | 服务端 | 9 | 10 | 5 |