数组的二分查找算法
Posted on Mon, 24 Nov 2025 14:15:14 +0800 by LiangMingJian
概述
二分查找算法,Binary Search Algorithm,是一种用在有序数组中,高效定位目标元素的方法。二分查找算法的核心是在每次查找过程中,将查找区间缩小一半,从而快速锁定目标位置。
动图解析
观察下述动图,第一行展示的是二分查找的过程,第二行展示的顺序查找的过程。不难发现,在有序数组中,二分查找的速度远比顺序查找的快速。
特别注意,二分查找是用在有序数组的算法。
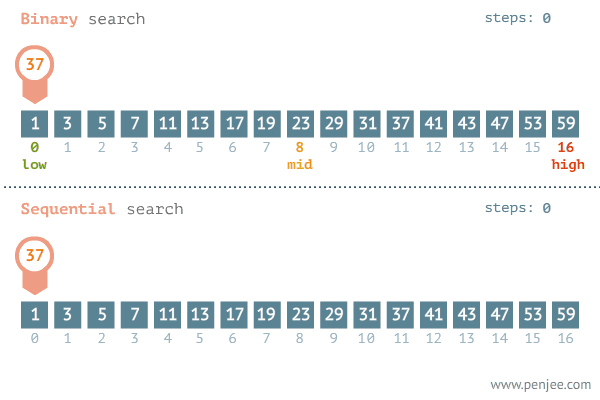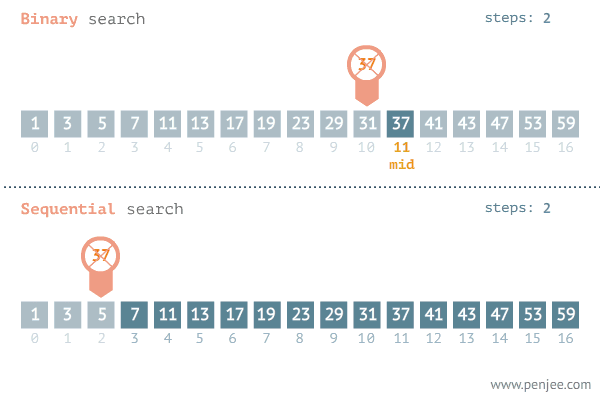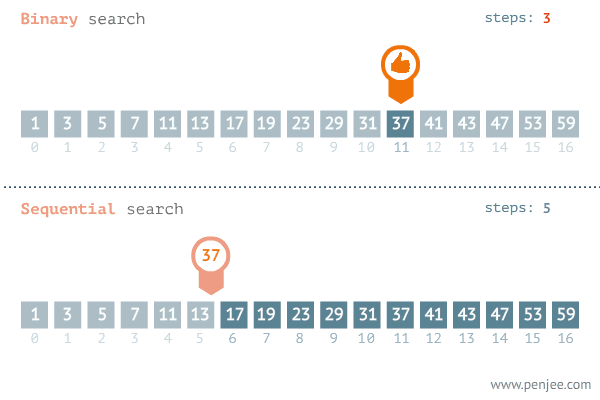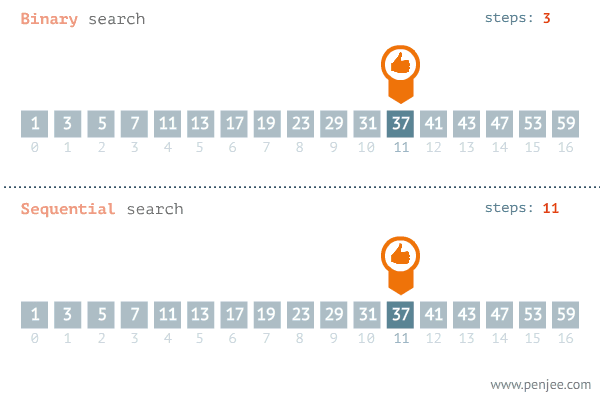
步骤分析
步骤一
初始化数组,确定待查找的数组或列表是有序的,确保元素已按升序或降序排列。
步骤二
设置一个查找区间,定义查找的左右边界。
在第一次查找时左边界 left 指向数组起始,右边界 right 指向数组末尾。
步骤三
通过公式 mid=(left+right)/2 计算查找区间的中间下标 mid(计算结果不要小数点)。
注意,这里是加法,用以求区间的中值。
步骤四
将目标值 target 与中间值 nums[mid] 进行比较,缩小区间。
- 如果目标值等于中间值,则找到目标值,返回序号 mid。
- 如果目标值小于中间值,则表明目标值在查找区间的左边,更新右边界为中间值序号减一,即
right=mid−1。 - 如果目标值大于中间值,则表明目标值在查找区间的右边,更新左边界为中间值序号减一,即
left=mid+1。
步骤五
重复步骤三和四,直到找到目标值(返回序号 mid),或查找区间为空(左边界 left 大于有边界 right 了,目标不存在)。
实现代码
from typing import List
def binarySearch(nums: List[int], target: int) -> int:
# 可选方法,判断数组是否升序
if not if_asc_sorted(nums):
return -1
# 设置查找区间的左右边界
left, right = 0, len(nums) - 1
# 循环查找区间,直到区间为空或者找到目标值
# 当左边界大于右边界时,[left, right] 区间为空
while left <= right:
# 计算中间位置 mid
# 可选:当 left 和 right 很大时,left + right 可能会超过整型 int 数据限制
# 因此可写为 left + (right - left) // 2 避免溢出
# (left+right)//2 = (2*left+right-left)//2 = left+(right-left)//2
# 上述可选公式与基础公式结果一致
mid = (left + right) // 2
# 若中间值等于目标值,则找到目标了,返回中间位置
if nums[mid] == target:
return mid
# 若中间值小于目标值,则目标在右半区间,收缩左边界
elif nums[mid] < target:
left = mid + 1
# 若中间值大于目标值,则目标在左半区间,收缩右边界
else:
right = mid - 1
# 区间为空,查找失败,返回 -1
return -1
def if_asc_sorted(nums: List[int]):
"""
可选方法,判断数组是否是升序的
实现逻辑:通过单行 for 语句构成的列表推导式,提取数组中每一个元素判断,
确保数组中每一个元素都比后一个元素小。
最后通过内置方法 all() 判断推导式返回对象中的所有元素是否都为 True。
"""
return all([nums[i] <= nums[i + 1] for i in range(len(nums) - 1)])
if __name__ == "__main__":
num = [1, 2, 3, 4, 5, 6, 7, 8, 9]
print(binarySearch(num, 6))
复杂度分析
- 时间复杂度:
O(logn),比顺序查找O(n)更高效。 - 空间复杂度:
O(1),只需要常数级别的额外空间。
————————————