数组的双指针算法
Posted on Tue, 25 Nov 2025 10:42:34 +0800 by LiangMingJian
概述
双指针算法,Two Pointers,是一种在遍历数组序列时,同时使用两个指针协同访问元素,以高效解决问题的一种算法。
常见双指针算法类型有以下三种:
- 适用于同数组序列相向移动的 「对撞指针」
- 适用于同数组序列同向移动的 「快慢指针」
- 适用于不同数组序列的 「分离双指针」
双指针算法的优势在于将暴力解法的时间复杂度 O(n²) 降至 O(n),避免重复扫描元素,减少不必要的循环,提高代码程序的效率。
对撞指针
对撞指针的算法逻辑
通过代码构造两个指针 left 和 right。其中,left 指针指向数组的开始位置,并向右移动;right 指向数组的结束位置,并向左移动。当两个指针相遇,即 left=right 时,返回结果。
对撞指针的示例图

对撞指针的实现逻辑
对撞指针在代码端的实现逻辑,大致分为以下四步:
- 构造两个指针变量
left = 0和right = len(nums)-1 - 构造一个
while left < right的循环,结束条件为left == right(两指针相遇) - 在循环内进行判断:
- 如果满足 A 条件,则将
left右移(left + 1); - 如果满足 B 条件,则将
right左移(right - 1); - 如果满足某个特殊条件,则直接返回结果
- 如果满足 A 条件,则将
- 循环直到两指针相遇或满足终止条件,此时算法结束
对撞指针常用于解决:有序数组或字符串的区间问题,比如查找特定元素对(两数之和)、回文判断、字符串反转等。
注意,对撞指针适用的数组必须是有序的。
示例:两数之和
给定一个单调递增的数组 [1, 2, 3, 4, 5, 6, 7, 8, 9, 10],数组中的每个元素只出现一次,且只能使用一次,要求找出这个数组中所有相加等于 13 的元素对,并返回包含所有元素对的数组。
from typing import List
def twoSum(nums: List[int], target: int) -> List[list]:
# 设置左右指针
left, right = 0, len(nums) - 1
# 设置结果数组
result = []
# 设置循环条件,结束条件为 left == right
while left < right:
total = nums[left] + nums[right]
# 如果元素和等于目标值,返回结果
# 因为数组是递增的且每个元素只出现一次,所以有:
# left+1 与 right 的元素和必定大于目标值
# left 与 right-1 的元素和必定小于目标值
# 此时,可以将右指针 right 左移,左指针 left 右移
if total == target:
result.append([nums[left], nums[right]])
right -= 1
left += 1
# 如果元素和大于目标值
# 因为数组是递增的且每个元素只出现一次,所以有:
# left+1 与 right 的元素和必定大于目标值
# left 与 right-1 的元素和小于或等于目标值
# 此时,只能将右指针 right 左移
elif total > target:
right -= 1
# 如果元素和小于目标值
# 因为数组是递增的且每个元素只出现一次,所以有:
# left+1 与 right 的元素和大于或等于目标值
# left 与 right-1 的元素和必定小于目标值
# 此时,只能将左指针 left 右移
else:
left += 1
return result
if __name__ == "__main__":
num = [1, 2, 3, 3, 4, 5, 6, 7, 8, 9, 10]
print(twoSum(num, 13))
# [[3, 10], [4, 9], [5, 8], [6, 7]]
示例:字符串反转
给定一个字符串 123456,要求将这个字符串反转为 654321,并返回这个字符串。
def stringReverse(target: str) -> str:
# 将字符串转换为数组
target_list = list(target)
# 设置左右指针
left, right = 0, len(target_list) - 1
# 设置循环条件,结束条件为 left == right
while left < right:
# 调换元素
temp = target_list[left]
target_list[left] = target_list[right]
target_list[right] = temp
# 左右指针移动
left += 1
right -= 1
return ''.join(target_list)
if __name__ == "__main__":
print(stringReverse('123456'))
快慢指针
快慢指针的算法逻辑
通过代码构造两个指针 fast 和 slow。这两个指针都从同一侧出发,但是快指针 fast 比慢指针 slow 移动更快速,两个指针以不同的速度遍历数组。当快指针到达末尾,或两指针相遇,或满足特定条件时,返回结果,算法结束。
快慢指针的示例图
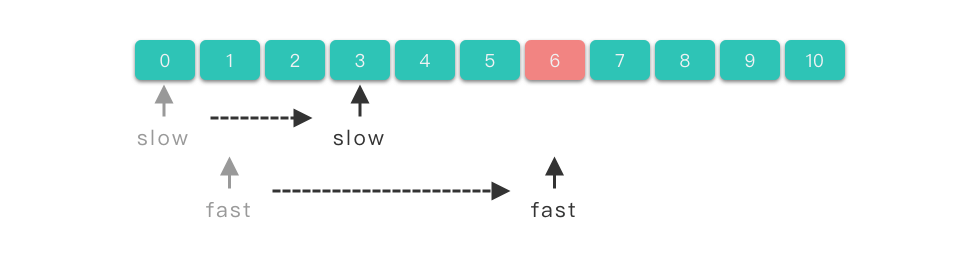
快慢指针的实现逻辑
快慢指针在代码端的实现逻辑,大致分为以下五步:
- 构造两个指针
slow=0, fast=1,分别指向第一第二个元素 - 构建一个
while的循环 - 循环的结束条件可以是:
- 快指针到达数组尾端
- 两个指针相遇了
- 满足特定的结束条件
- 在循环内判断:满足条件时,慢指针移动指针,不满足时快指针移动
- 循环直到满足终止条件,此时算法结束
快慢指针适用于解决:数组元素的移动和删除问题,比如移动零,有序数组去重等。
示例:移动零
给定一个含 0 数组 [0, 1, 2, 3, 0, 0, 6, 5, 4],要求将数组中所有的 0 移动到数组的最后面,返回处理后的数组。
from typing import List
def moveZeroes(nums: List[int]) -> List[int]:
# 设置快慢指针
slow, fast = 0, 1
# 获取数组长度
length = len(nums)
# 构建循环,默认结束条件为快指针到达数组结尾
while fast < length:
# 如果快指针所在值不等于 0,则交换快慢指针元素,将非零元素移动到数组前面
# 然后移动慢指针以接收下一个非零值,重复交换后,0 会聚集在数组末尾
if nums[fast] != 0:
nums[slow], nums[fast] = nums[fast], nums[slow]
slow += 1
# 无论是否交换,快指针要遍历所有的元素
fast += 1
return nums
if __name__ == "__main__":
num = [0, 1, 2, 3, 0, 0, 6, 5, 4]
print(moveZeroes(num))
示例:有序数组去重
给定一个包含重复元素的有序数组 [1, 1, 1, 2, 2, 3, 4, 5],要求将这个数组去重,返回去重后的数组。
快慢指针对于数组的去重只能应用于有序数组。
from typing import List
def removeDuplicates(nums: List[int]) -> List[int]:
# 设置快慢指针
slow, fast = 0, 1
# 获取数组长度
length = len(nums)
# 构建循环,默认结束条件为快指针到达数组结尾
while fast < length:
# 如果快指针指向的元素和慢指针指向的元素不同
# 说明遇到了新的不重复元素
if nums[slow] != nums[fast]:
# 此时,慢指针必须要前进一位,用来存储新的元素
slow += 1
# 将快指针指示的新元素赋值到新的慢指针位置
nums[slow] = nums[fast]
# 无论是否交换,快指针要遍历所有的元素
fast += 1
# 返回去重后的数组( 下标从 0 开始,所以要 +1 )
return nums[:slow+1]
if __name__ == "__main__":
num = [1, 1, 1, 2, 2, 3, 4, 5]
print(removeDuplicates(num))
# [1, 2, 3, 4, 5]
分离双指针
分离双指针的算法逻辑
通过代码构造两个指针 left_1 和 left_2。这两个指针分别位于两个不同的数组,这两个指针独立在各自数组中运行移动,协同完成任务。
分离双指针的示例图
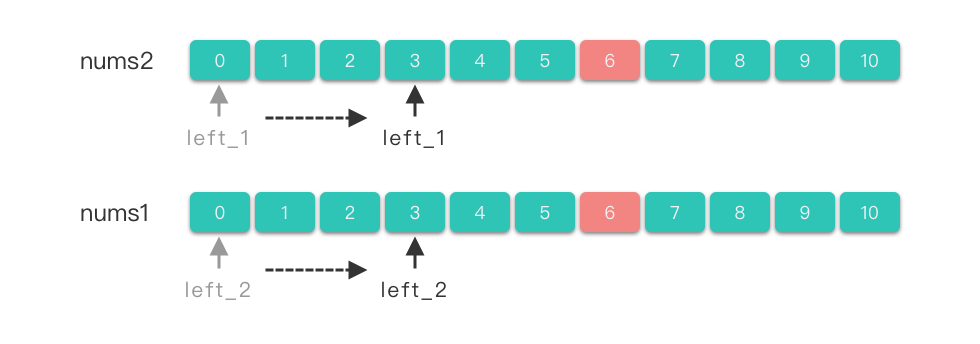
分离双指针的实现逻辑
分离双指针在代码端的实现逻辑,大致分为以下四步:
- 构造两个指针
left_1和left_2,分别指向各自数组的起始位置 - 构造一个
while循环,结束条件为任意一个指针到达数组末尾 - 在循环内根据条件同时移动两个指针,或只移动某一个指针
- 循环直到满足终止条件,此时算法结束
分离双指针主要应用于有序数组的合并、交集、并集等问题,能够高效地同时遍历两个数组,协同完成元素的比较与处理。
分离双指针适用的数组必须是有序的!
示例:求两个数组的交集
给定两个数组 [1,2,2,1,3,4] 和 [2,2,3,4],要求计算这两个数组的交集,重复元素只计算一次,返回计算的交集数组。
from typing import List
def intersection(nums1: List[int], nums2: List[int]) -> List[int]:
# 分离双指针适用的数组必须有序,所以需要先排序
nums1.sort()
nums2.sort()
# 构造分离双指针
left_1, left_2 = 0, 0
# 构造结果数组
res = []
# 构造循环,结束条件为任意一个指针到达对应数组结尾
while left_1 < len(nums1) and left_2 < len(nums2):
# 当双指针对应元素相等时,写入结果数组
# 然后双指针分别向后移动
if nums1[left_1] == nums2[left_2]:
# 只有 res 为空或当前元素与上一个加入的元素不同才加入结果,避免重复
# (因为数组是有序的,所以结果去重只需判断上一个加入的元素即可)
if not res or nums1[left_1] != res[-1]:
res.append(nums1[left_1])
left_1 += 1
left_2 += 1
# 当 1 指针对应元素小于 2 指针时
# 将 1 指针后移(因为有序,所以 1 数组后一个元素比前一个大)
elif nums1[left_1] < nums2[left_2]:
left_1 += 1
# 当 2 指针对应元素小于 1 指针时
# 将 2 指针后移(因为有序,所以 2 数组后一个元素比前一个大)
else:
left_2 += 1
return res
if __name__ == "__main__":
num1 = [1,2,2,1,3,4]
num2 = [2,2,3,4]
print(intersection(num1, num2))
# [2, 3, 4]
示例:求两个数组的并集
from typing import List
def union(nums1: List[int], nums2: List[int]) -> List[int]:
# 分离双指针适用的数组必须有序,所以需要先排序
nums1.sort()
nums2.sort()
# 构造分离双指针
left_1, left_2 = 0, 0
# 构造结果数组
res = []
# 构造循环,结束条件为任意一个指针到达对应数组结尾
while left_1 < len(nums1) and left_2 < len(nums2):
# 当双指针对应元素相等时,写入结果数组,然后双指针分别向后移动
if nums1[left_1] == nums2[left_2]:
# 只有 res 为空或当前元素与上一个加入的元素不同才加入结果,避免重复
# 因为数组是有序的,所以结果去重只需判断上一个加入的元素即可
if not res or nums1[left_1] != res[-1]:
res.append(nums1[left_1])
left_1 += 1
left_2 += 1
# 当 1 指针对应元素小于 2 指针时,将 1 指针后移
# 因为有序,所以 1 数组后一个元素比前一个大
# 因为要计算并集,所以要添加这个元素
elif nums1[left_1] < nums2[left_2]:
# 去重
if not res or nums1[left_1] != res[-1]:
res.append(nums1[left_1])
left_1 += 1
# 当 2 指针对应元素小于 1 指针时,将 2 指针后移
# 因为有序,所以 2 数组后一个元素比前一个大
# 因为要计算并集,所以要添加这个元素
else:
# 去重
if not res or nums2[left_2] != res[-1]:
res.append(nums2[left_2])
left_2 += 1
# 处理剩余元素
while left_1 < len(nums1):
if not res or nums1[left_1] != res[-1]:
res.append(nums1[left_1])
left_1 += 1
while left_2 < len(nums2):
if not res or nums2[left_2] != res[-1]:
res.append(nums2[left_2])
left_2 += 1
return res
if __name__ == "__main__":
num1 = [1,2,2,1,3,4,6]
num2 = [2,2,3,4,5]
print(union(num1, num2))
# [1, 2, 3, 4, 5, 6]
拓展阅读
为什么对撞指针和分离双指针都要有序数组?
对撞指针和分离双指针在对数组使用时,需要数组是有序的,这主要是因为有序的数组可以为指针的移动提供确定性方向,让指针移动有据可依。
在有序数组中,对撞指针可以根据当前元素和与目标值的大小关系,确定性地移动左指针或右指针。但如果是无序指针,则会无法确定指针的移动方向,比如下述示例:
list1 = [3, 7, 1, 9, 2]
target = 10
当左指针为 0(对应值 3),右指针为 4(对应值 2),按对撞指针算法有:
- 若按左值大于右值时,移动左指针的逻辑,此时左指针会移动到 1(对应值 7),结果会导致丢失组合(3+7)
- 若按左值大于右值时,移动右指针的逻辑,此时右指针会先移动到 3(对应值 9),对应值 9 大于 3,然后接着还是要移动左指针到 1(对应值 7),结果还是会导致丢失组合(3+7)
从上面的示例不难看出,有序数组能避免对撞指针发生这种问题,确保每种组合都被正确检查,给指针的移动提供确定性方向。
在分离双指针中,有序数组保证了两个数组元素的可比较性,比如下述示例:
list1 = [3,2,1]
list2 = [1,2]
按分离双指针算法有:
- 若按 1 指针大于 2 指针,1 指针移动逻辑,1 指针移动到 2(对应值 1)时,2 指针还是在 0(对应值 1),然后 1 数组会遍历完成,算法结束,2 数组会出现遗漏。
- 若按 1 指针大于 2 指针,2 指针移动逻辑,2 指针移动到 1(对应值 2)时,1 指针还是在 0(对应值 1),然后 2 数组会遍历完成,算法结束,1 数组会出现遗漏。
同样的,与对撞指针一样,如果分离双指针应用到无序数组,其结果会导致遗漏。
以上便是为什么对撞指针和分离双指针都要有序数组的原因。
————————————