Python 的集合
Posted on Mon, 29 Sep 2025 15:22:23 +0800 by LiangMingJian
前言
集合是由确定且互不相同的对象(称为元素)构成的整体。在 Python 中集合是一个无序且内部元素不重复的数据结构。
集合支持的操作与列表,元组,字典等基本一致。比如都支持使用 len 获取长度;支持用 in 和 not in 检查元素存在与否;以及支持 for 循环迭代集合对象。
需要注意的是,集合元素的读取只能通过循环遍历。这是因为集合本身是无序的,所以不可以像列表或元组一样进行索引或切片操作。同时因为没有键值对的关系,所以不可以通过键来获取集合中元素。
集合的创建
集合在 Python 中的表现类似于字典,同样是使用大括号 {} 对元素进行包裹。但不同之处在于,集合没有键,而字典有键。
特别注意,在创建空集合的时候只能使用 s = set(),这是因为 {} 会被 Python 识别为一个空字典。
# 这是字典
s1 = {'name': 'Python', 'age': 20}
# 这是集合
s2 = {'Python', 20}
# 这是空字典
s3 = {}
# 这是空集合
s4 = set()
另外,对于方法 set(),支持传入一个可迭代对象如列表,元组,字典。
该方法会自动剔除传入对象里面的重复元素,然后将结果转换为一个集合输出(对于字典,则只会提取并处理键对象)。
s1 = set([1, 2, 2, 3])
s2 = set((1, 2, 3, 3))
s3 = set({'name': 'Python', 'age': 20})
print(s1) # {1, 2, 3}
print(s2) # {1, 2, 3}
print(s3) # {'age', 'name'}
集合元素的添加
add(obj)
添加一个新的元素,如果元素已存在,则忽略,不会出现报错。
s1 = set()
# 添加元素
s1.add(1)
print(s1)
# {1}
# 再次添加元素,此时元素已存在,忽略
s1.add(1)
print(s1)
# {1}
集合元素的删除
在集合中,提供 4 种方式来移除元素。
remove(obj)
删除一个指定的元素,如果元素不存在则会报错
s1 = {1, 2, 3}
s1.remove(4)
# KeyError: 4
discard(obj)
删除一个指定的元素,如果不存在,则忽略,不出现报错。
s1 = {1, 2, 3}
s1.discard(4)
# 正常结束
pop()
随机抛出一个元素,然后从集合中移除这个元素。
s1 = {1, 2, 3}
data = s1.pop()
print(data) # 1
print(s1) # {2, 3}
clear()
清空整个集合,但不会删除集合对象。
s1 = {1, 2, 3}
s1.clear()
print(s1) # set() 空集合
集合的运算
集合在数学计算中支持并集,交集,差集等运算方法。在 Python 中,同样支持通过关键字对集合对象实现上述运算。
并集
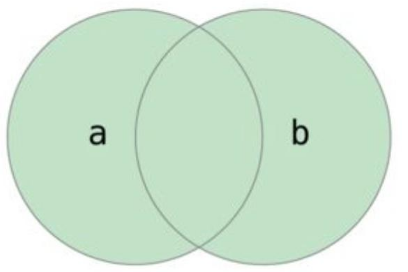
两个集合的并集,记作 $A \bigcup B$,是指所有属于 A 或 B 或两者的元素组成的集合。
在 Python 中,通过方法 union() 和 update() 实现并集运算,区别在于 union 会返回一个新的集合,而 update 会在原集合上修改。
s1 = {1, 2, 3, 4}
s2 = {3, 4, 5, 6}
# s1 求与 s2 的并集
s3 = s1.union(s2)
print(s3)
# {1, 2, 3, 4, 5, 6}
# 更新 s1 为 s1 和 s2 的并集
s1.update(s2)
print(s1)
# {1, 2, 3, 4, 5, 6}
交集
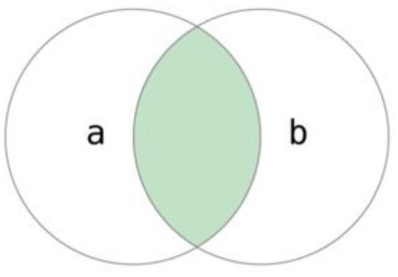
两个集合的交集,记作 $A \bigcap B$,是指所有属于 A 又属于 B 的元素组成的集合。
在 Python 中,通过方法 intersection() 和 intersection_update() 实现交集运算,区别在于 intersection 会返回一个新的集合,而 intersection_update 会在原集合上修改。
s1 = {1, 2, 3, 4}
s2 = {3, 4, 5, 6}
# s1 求与 s2 的交集
s3 = s1.intersection(s2)
print(s3)
# {3, 4}
# 更新 s1 为 s1 和 s2 的交集
s1.intersection_update(s2)
print(s1)
# {3, 4}
特别的,存在方法 isdisjoint() 判断两个集合是不是不相交并(disjoint union,可以用来判断是否存在交集),如果是不相交并(没有交集)则返回 True,如果不是不相交并(有交集)则返回 False。
s1 = {1, 2, 3, 4}
s2 = {3, 4, 5, 6}
# s1 和 s2 是不是不相交并
print(s1.isdisjoint(s2))
# False
差集
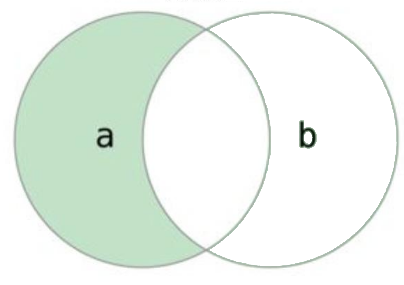
两个集合的差集,记作 $A — B$,是指属于 A 但不属于 B 的元素组成的集合。
在 Python 中,通过方法 difference() 和 difference_update() 实现差集运算,区别在于在于 difference 会返回一个新的集合,而 difference_update 会在原集合上修改。
s1 = {1, 2, 3, 4}
s2 = {3, 4, 5, 6}
# s1 求与 s2 的差集
s3 = s1.difference(s2)
print(s3)
# {1, 2}
# 更新 s1 为 s1 和 s2 的差集
s1.difference_update(s2)
print(s1)
# {1, 2}
对称差集
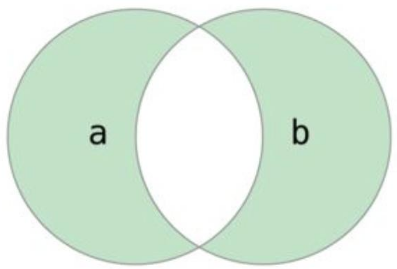
两个集合的对称差集,记作 $A \bigoplus B$,是指属于 A 但不属于 B ,与属于 B 但不属于 A 的元素组成的集合。
在 Python 中,通过方法 symmetric_difference() 和 symmetric_difference_update() 实现对称差集运算,区别在于在于 symmetric_difference 会返回一个新的集合,而 symmetric_difference_update 会在原集合上修改。
s1 = {1, 2, 3, 4}
s2 = {3, 4, 5, 6}
# s1 求与 s2 的对称差集
s3 = s1.symmetric_difference(s2)
print(s3)
# {1, 2, 5, 6}
# 更新 s1 为 s1 和 s2 的对称差集
s1.symmetric_difference_update(s2)
print(s1)
# {1, 2, 5, 6}
子集判断
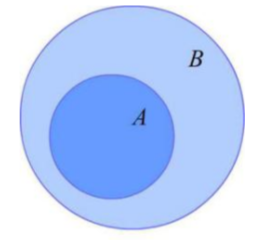
如果一个集合 A 的元素完全属于在另外一个集合 B,则可以称这个集合 A 是集合 B 的子集,记作 $A \subseteq B$ 。
在 Python 中,支持通过 issubset() 来判断一个集合是不是另外一个集合的子集。
s1 = {1, 2}
s2 = {1, 2, 3, 4}
# 判断 s1 是不是 s2 的子集
print(s1.issubset(s2))
# True
超集判断
超集是子集的逆关系,如果一个集合 A 的元素完全包含另外一个集合 B 的所有元素,则可以称为这个集合 A 是集合 B 的超集,记作 $A \supseteq B$ 。
在 Python 中,支持通过 issuperset() 来判断一个集合是不是另外一个集合的超集。
s1 = {1, 2}
s2 = {1, 2, 3, 4}
# 判断 s2 是不是 s1 的超集
print(s2.issuperset(s1))
# True
拓展阅读:集合运算符
在 Python 中,集合的运算除了使用上述的方法外,还支持使用 in, not in, |, &, <, > 等操作符来进行计算。
支持的操作符内容如下:
| 操作符 | 示例 | 说明 |
|---|---|---|
| x in set | 1 in {1,2} | 成员判定 |
| x not in set | 1 not in {1,2} | 成员判定 |
| set <= other | {1,2} <= {1,2,3,4} | 子集判定 |
| set < other | {1,2} < {1,2,3,4} | 真子集判定(真子集不止包含子集的元素,还包含子集没有的元素) |
| set >= other | {1,2,3,4} >= {1,2} | 超集判定 |
| set > other | {1,2,3,4} > {1,2} | 真超集判定(真超集不止包含子集的元素,还包含子集没有的元素) |
| set | other | {1,2} | {2,3} => {1,2,3} | 并集,等价于 union() |
| set |= other | set |= {2,3} | 并集,等价于 update() |
| set & other | {1,2} & {2,3} => {2} | 交集,等价于 intersection() |
| set &= other | set &= {2,3} | 交集,等价于 intersection_update() |
| set - other | {1,2} - {2,3} => {1} | 差集,等价于 difference() |
| set -= other | set -= {2,3} | 差集,等价于 difference_update() |
| set ^ other | {1,2} ^ {2,3} => {1,3} | 合并不同项,等价于 symmetric_difference() |
| set ^= other | set ^= {2,3} | 等价于 symmetric_difference_update() |